11 November 2023

This post announces the second public release of the GNU Aris in WebAssembly project. The project was financially supported by Google (in the frame of the Google Summer of Code 2023 programme). The code was improved by Saksham Attri, a university student from India. His work was rather complicated: he had to use bleeding edge technologies like Qt 6 and emscripten, and create a WebAssembly port of libxml2. Saksham was extremely diligent and very ambitious during the three months long project. It was great to work with him.

My part was to help him during this project. On behalf of GNU I helped him to finalize some very important improvements to get GNU Aris work in a web environment, including mobile phones. This is quite important for a large amount of possible users, including prospective mathematics teachers and students. My co-mentors Alexander Thaller and Andreas Ebetshuber (both are my former students) also helped us to get these things work.

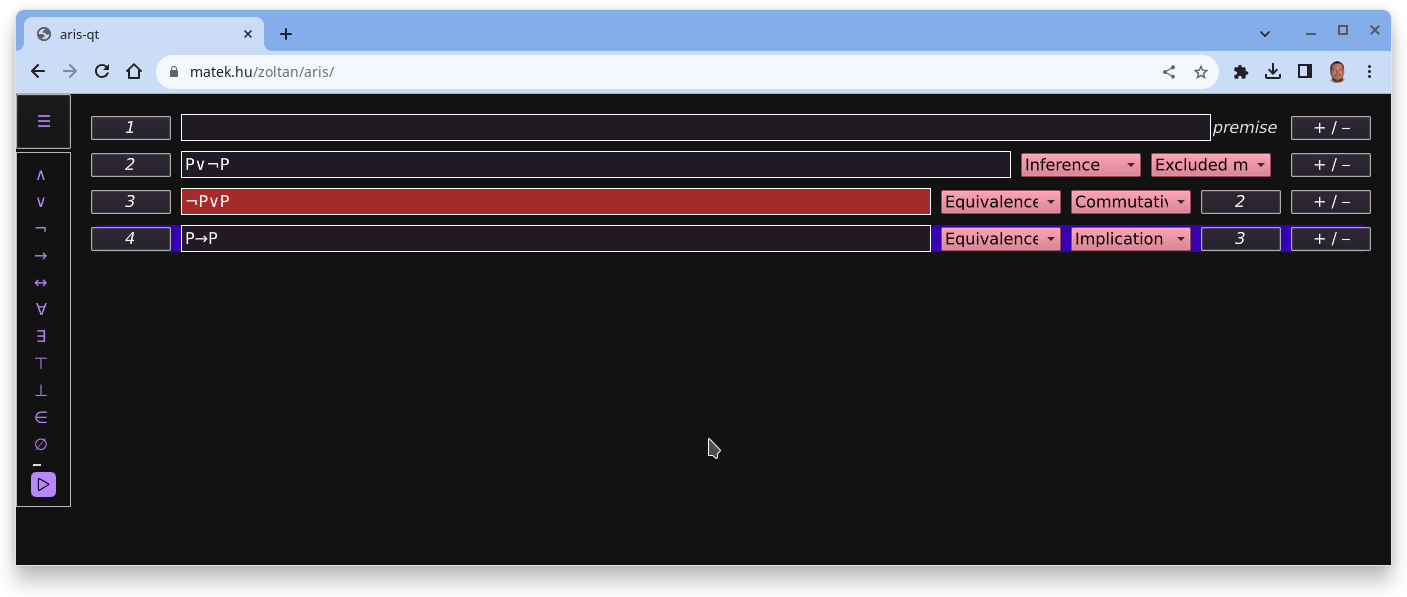
I will not go in the technical details in this short entry. If you are interested, please go to Saksham's summary and read his final submission. Today's version (which has minor improvements in the user interface) can be tried here. (If you want to create the example shown above, add a conclusion by using the button +/-, type P∨¬P on line 2, set Inference and Excluded middle on the right, then create another conclusion on line 2. Now you have line 3, enter ¬P∨P and set Equivalence and Commutativity on the right and press button 2 on the left. Finally create another conclusion on line 3. You will have line 4, enter P→P, set Equivalence and Implication and press button 3 on the left. The ▷ button will check if your proof is correct.)

The official version will hopefully be regularly updated at matek.hu/kovzol/aris.

These are the most important features that were added by Saksham:

• Full redesign of the user interface by using Qt 6 Quick and QML.
• Web based interface if the software is built via emscripten to WebAssembly.
• Dark mode.

Some further features like updating icons (for dark mode), possibility to setting the language of the user interface, adding a SAT solver, and exporting a derivation tree, are planned. In case you want to give the web version a try, you can select a .tle file from the proof folder of the documentation and open it on the webpage. Then click on the ▷ button to check if the proof is correctly constructed!