17 November 2020
Offsets of a trifolium
It is always amazing to work together with enthusiastic mathematicians.
One of my current projects is a joint research with
Prof.
Noah Dana-Picard,
president of
Jerusalem
College of Technology. Our recent work is on studying offsets of various algebraic curves.
In the most recent study we focus on the offsets of a trifolium.
What is a trifolium? Well, this is a simple question: It is a kind of
rose
curve that has three leaves. From the algebraic point of view, it is the curve
\[\left(x^2+y^2\right)^2=ax(x^2-3y^2),\]
here we assume that \(a=1\) without loss of generality.
What is an
offset curve?
Let us imagine that we move a circle on an other curve by putting its
center directly on the curve, and the circle has a fixed diameter. We are interested in the
envelope of all possible circles that can be drawn in this way.
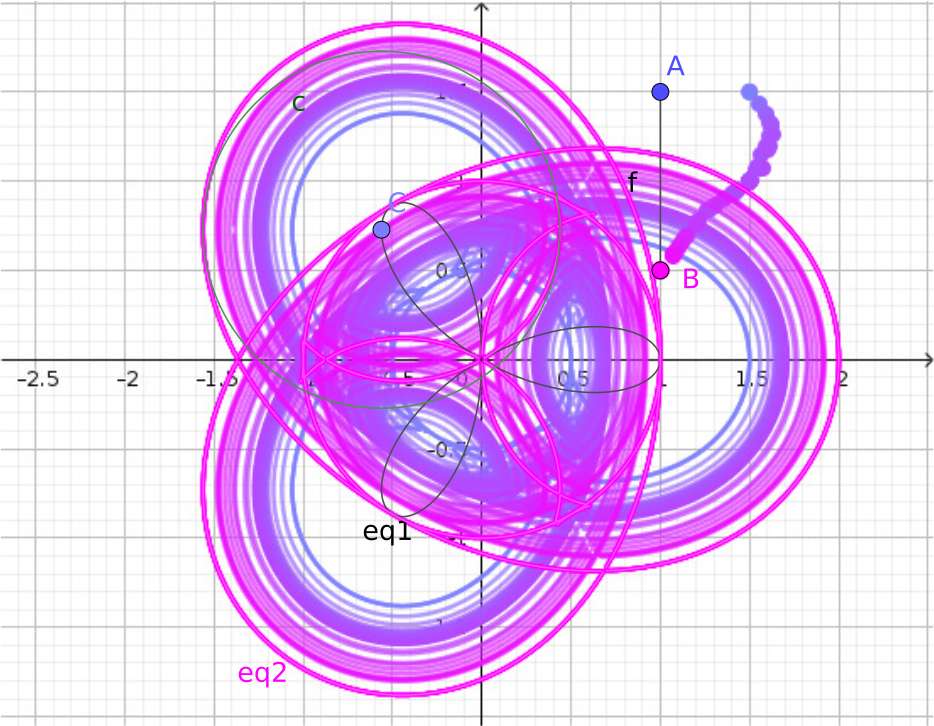
The following GeoGebra applet (actually it is constructed in GeoGebra Discovery)
helps understanding the idea. What is more, it can be computed by strict mathematical means
that the envelope curve is of degree 14.
You may want to carefully drag point \(A\) or \(B\) to change the diameter of the curve from 1 to
a different value. Depending on the speed of your machine and your luck you may obtain some
other curves, but most of them will be still of degree 14.
If you are unlucky, the computation gets too heavy and you need to close this tab
in your browser to avoid your system to be unresponsive and eventually hang! Anyway,
you have been warned: research is sometimes a difficult thing and requires risking danger.
In the figure at the top of this page you can see a successful attempt to show
several offset curves at the same time. The radii of the circles vary from \(0.5\) to \(1\).
You may find that the obtained curve in the Algebra View is of degree 16. You are right,
but it is actually a product of two polynomials: the offset curve (of degree 14) and a circle
(of degree 2). The algorithm offered by GeoGebra finds both, because the inmost envelope, a circle,
is not removed from the result.
Continue reading…
See also a filtered list of the entries on topics
GeoGebra,
technical developments or
internal references in the Bible.

|
Zoltán Kovács
Linz School of Education
Johannes Kepler University
Altenberger Strasse 69
A-4040 Linz
|