A LEGO kit for prospective math teachers
Advances in STEAM Education, looking for future synergies
19th April 2022
by Zoltán Kovács

Abstract
A report is given on a part of an undergraduate level course "Computer aided mathematics education 2",
held in the winter semester of the academic year 2021/2022 by the author, at
The Private University College of Education of the Diocese of Linz,
Austria. A set of 20 students, prospective mathematics teachers, studied 4-bar linkages
and other geometric constructions and their mathematical background
with the help of a LEGO kit, assembled by the author. The report gives an overview on how the topic was
introduced and developed, and which other means were additionally used. Some parts of the covered topics
and the outcome of the course may also be introduced (directly or indirectly) in secondary (or eventually,
even primary) education level to focus on STEAM concepts.
A rocking horse camel... – an introductory (?) example

This is a toy exhibited in a medical center in
Freistadt, Upper Austria.
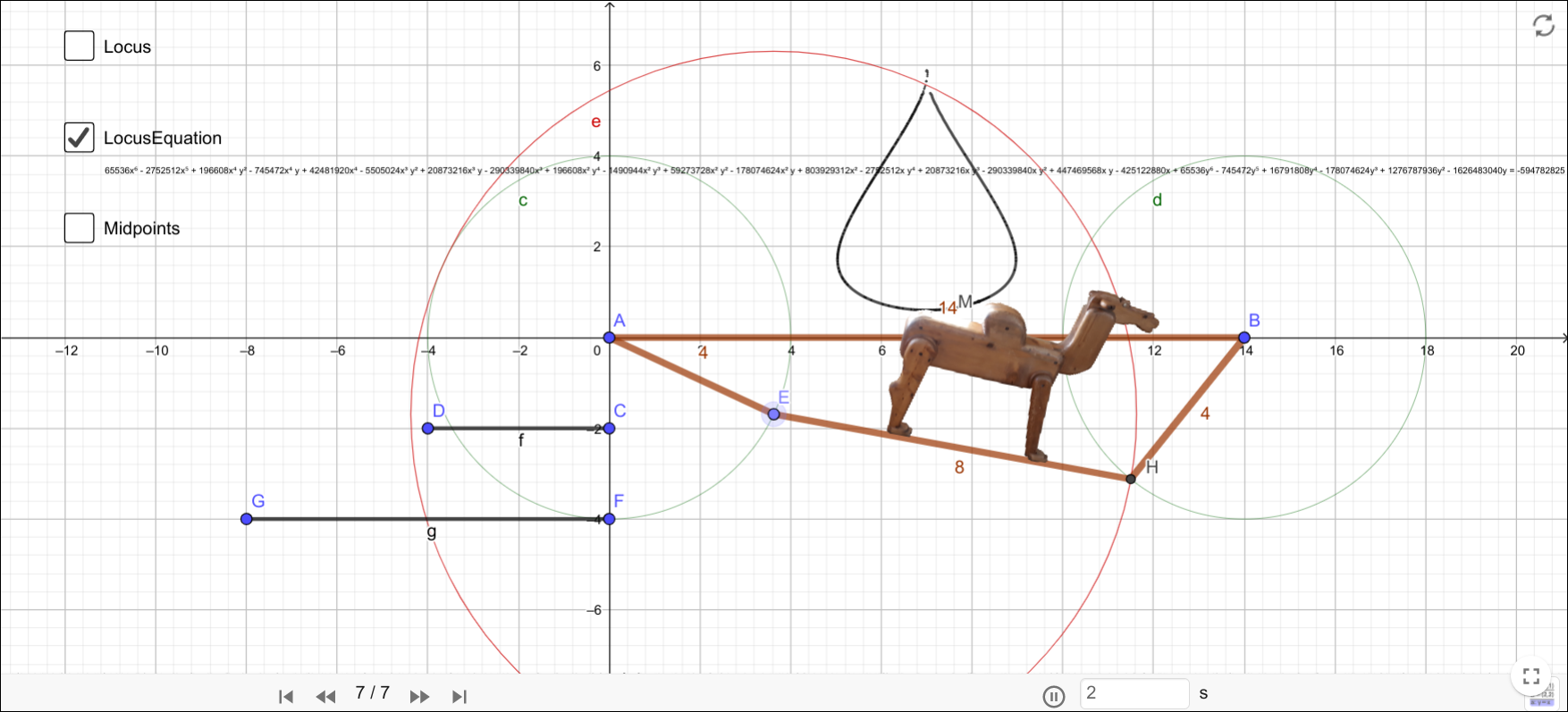
As an introductory example of non-trivial movements I drew this rocking camel into the attention
of my students (future secondary school teachers),
by asking: what curve can describe the movement of the hump of the camel?
Answering this question consisted of the following steps:
- Making exact measurement of the toy and its parts (by me, using photos and a measuring tape).
- Model the toy in GeoGebra and trace the movement of the hump.
- Make a conjecture.
- Show the locus of the trace points.
- Make a second conjecture.
- Compute the mathematical equation of the locus.
- Check the conjectures.
- Generalize the problem with different inputs.
First: some technical, then: some didactical comments to the applet
- To analyze the applet, first scroll down to the Navigation Bar and go back to the 0th step.
- Steps 1 and 2 define the length for the two equal long bars of the toy linkage.
- Steps 3 and 4 draw three circles c, d and e. While points A and B are freely chosen, point E is constrained on circle c, and point H is an intersection of d and e.
- Steps 5 and 6 create the skeleton and a 2D image model of the camel.
- Step 7 shows the point M that corresponds to the top of the hump of the camel (approximately).
- Dragging the point E makes the toy moving, and most interestingly, the point M moves together with the drawing, and its trace can be observed by the user.
- Most students in my lecture conjectured that the achieved curve is an ellipse. By dragging point E near the position \((0,5.5)\) that this is not the case!
- Clicking again on the ▶▶ button three checkboxes appear on the top-left of the applet. The first one, Locus shows all possible points that can be reached by a simple dragging of point E.
- Interestingly enough, the linkage has an external position that can be reached either near points \((-2,5)\) and \((-2,-5)\) when dragging E close to these two points. When dragging point E back, the movement changes to a second track. Altogether the union of the two traces seems to build a strange 8-form.
- By checking the option LocusEquation, the user obtains a closed curve, containing both tracks of point E at the same time. Also, a surprisingly complicated equation is shown.
- By selecting the third option Midpoints, the user may get an idea how the hump point M was created: First the midpoint I (of segment EH) was constructed, then a rotation of E about I by 90 degrees yields point E', then J is another midpoint of segment E'I, K is the midpoint of E'J, L is the midpoint of E'K, and M is the midpoint of KL. (By using this technique, any point of the camel can be arbitrarily approached, only by using midpoints. Midpoints are easy to create and simple to compute, that's why we use them here.)
- A generalization of the movement (by using some specific inputs) may result in simpler curves. For example, the input \(B=(14,0)\), \(D=(-4,0)\), \(G=(-8,0)\) (all other data remain the same as before) gives an equation that is still long, but, at least, it fits the screen. One can learn that this curve is of degree 6 (a sextic), so a general conjecture can be (after more playing and dragging) that most outputs for such linkages result in sextics.
Something simpler and handier: a LEGO kit!
It may be difficult to buy or build a rocking horse or camel. A more affordable option is to
order some LEGO bricks from the Internet and build our own linkages as a do-it-yourself activity.
It is cheaper to order more parts in the same package, so I planned for 20 students and
created a shopping list to find the best colors for the best price and value. This is a challenging
task, because some shops have just a very limited number of bricks, or just a few colors,
or, sometimes, the prices are quite high.
Finally, some weeks before Christmas 2021, in the very middle of the pandemic and therefore
online education, I managed to assemble an "official" bag of LEGO bricks to study linkages.
The resulted LEGO kit can be considered as an improvement of one
of my former projects.


To avoid delivery costs, I left the bags at the reception of the university college,
so everybody could pick up a bag for further self-experimenting at home. Later I asked
the students to either pay for the bag if they think it is fun and useful (as a total of 10 EUR) or return
it to the reception at the end of the semester. (Only 3 bags have been returned.)
Shopping list
| No. | Item | Quantity |
| 1 | Green Baseplate 16x16 (6098) | 1 |
| 2 | Yellow Brick 1x6 (3009) | 1 |
| 3 | Yellow Brick 1x8 (3008) | 1 |
| 4 | Blue Brick 1x6 (3009) | 1 |
| 5 | Blue Brick 1x8 (3008) | 1 |
| 6 | Blue Brick 1x1 (3005) | 1 |
| 7 | White Brick 1x6 (3009) | 1 |
| 8 | White Brick 1x8 (3008) | 1 |
| 9 | Reddish Brown Brick 1x1 (3005) | 1 |
| 10 | Reddish Brown Brick 1x6 (3009) | 2 |
| 11 | Red Brick 2x4 (3001) | 4 |
| 12 | Blue Tile 1x4 (2431) | 1 |
| 13 | Yellow Tile 1x4 (2431) | 1 |
| 14 | Red Brick 1x2 (3004/93792) | 2 |
| 15 | Dark Stone Gray Beam 1 (18654) | 2 |
| 16 | Medium Stone Gray Beam 3 (32523) | 1 |
| 17 | White Beam 5 (32316) | 3 |
| 18 | Black Beam 6x0.5 (28570/32063) | 4 |
| 19 | Yellow Beam 9 (40490/64289) | 2 |
| 20 | Dark Stone Gray Beam 11 (32525/64290) | 2 |
| 21 | Red Beam 15 (32278/64871) | 1 |
| 22 | Black Technic Pin with Friction Ridges and Slots (2780/61332) | 9 |
| 23 | Blue Long Pin with Friction (6558/42924) | 3 |
Additionally, I put two pen refills (a G2 and an A2)
in the bag. By using these parts we were able to study a larger set of linkages before and
after the Christmas holidays, altogether in 6 weeks.
Student activities for 6 weeks (90 minutes each)
- In the first week some discussion for the rocking camel movement was begun. Nice homework assignments were submitted like this one.
- In the second week the conjectures were discussed in detail and some generalization issues were asked. I invited the students to construct Watt's linkage that creates a smart 8-form.
- By using a former idea we built the Ellipsograph of Archimedes. Also, the activity Cat on a ladder was discussed – it is equivalent to the dynamics of the ellipsograph. We also studied the algebraization steps of a geometric figure, and how computer algebra can help in factorizing polynomials in two variables, and why elimination of variables in a set of equations can be helpful when solving some related problems. Finally I asked the students to install LEGO Digital Designer (LDD) for the next week on their home PCs.
- We built Chebyshev's linkage by using the LEGO kit. It produces a variant of the curve that describes the hump of the camel, but a part of it seems to be completely straight. We zoomed into the plot and learned that the Chebyshev curve does not produce a straight line, even if seemingly this is the case. After a more precise definition of the 4-bar linkages I asked if there is an input where – even if the output is a sextic – the movement polynomial can be factorized into 3 polynomials. (This is a very interesting question that is far from being trivial. Via experimenting, one can learn that finding 2 factors leads to a circle and a quartic, a so-called Cassini oval; and 3 factors always correspond to three circles. This also implies that there is no way to draw a completely straight line by using a 4-bar linkage.)
- We used LDD to build Hart's A-frame.
At the same time, we also built the linkage with the LEGO kit. By setting up an equation system
we started to translate the geometric problem into an algebraic setting.
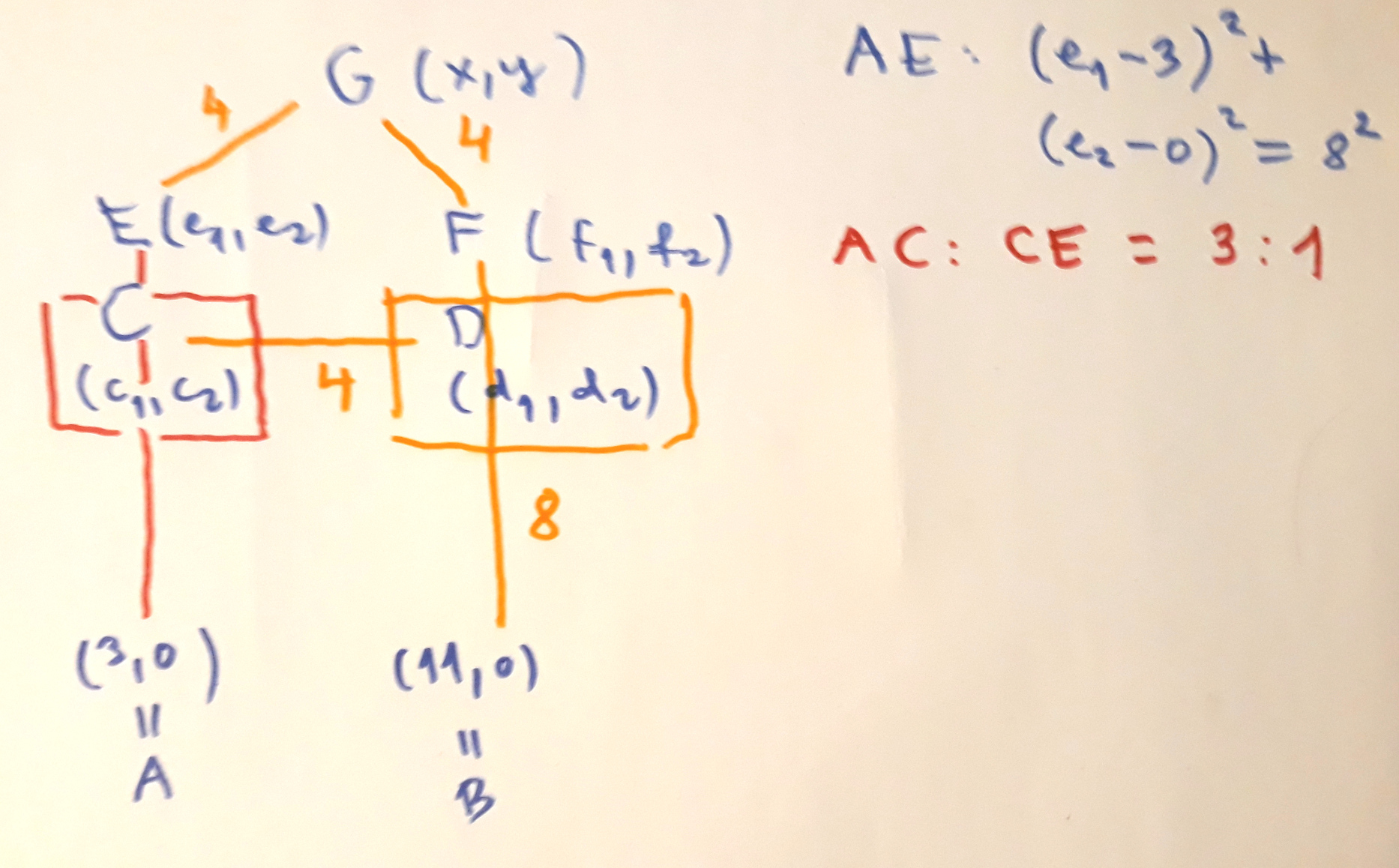
As a homework assignment, the students were asked to complete the algebraization and eliminate all variables but x and y from the set of obtain equations. (The result is a septic. We require a factorization to see that a sextic and a linear component are multiplied, and therefore, the union of a sextic curve and a line will appear.) Also, a GeoGebra construction was asked to create that visualizes the motion of Hart's A-frame. - During the last week we discussed and solved the homework assignments, and made some steps towards the illustration on how a computer algebra algorithm (namely, Buchberger's method) can support elimination of some variables in a set of polynomial equations.
A summary
The problem setting with the movement of the hump of a camel seems simple, but the answer is
surprisingly difficult – if we consider a 6th degree polynomial somewhat off-topic in the regular
school system. On the other hand, this supports that STEAM problem assignments should not necessarily
be very simple, and real life problems can indeed require additional scientific background.
The problem of the ellipsograph can be considered more standard, and has a huge
literature.
Even though, its study by using a computer is not very straightforward, and can be challenging
for the students. I personally find this activity a possible task even for younger learners as an
achievable challenge, because the equation of an ellipse is not so far away from the typical curriculum.
Precise drawing of a continuous (and hence beautiful) curve can be an artistic challenge as well – here the "A" in
the STEAM concept can also be highlighted.
The "A" in the STEAM concept can also be an important part when finding beautiful sextic curves
by random experiments. I emphasize here that the geometry of the sextic curves is not yet completely
classified. (Some experts say that even the quartics
are not yet completely categorized.)
The lack of completeness also raises challenges in engineering ("E"), by calling for better
quasi-linear motions than Watt's and Chebyshev's linkages can offer.
Clearly, technology ("T") played an important role during the activities. GeoGebra is unavoidable
in sketching, investigating (if the curves are indeed non-linear) and analyzing the algebraic
system in the background.
All of these activities can be considered as a real scientific ("S") work, not just for these
future mathematics students, but – hopefully – for their future learners who can play
and do researching at the same time with non-trivial, recent problems.
From the educational point of view, however, the concept can be criticized.
There is obviously some non-trivial mathematics in the background.
A teacher needs to define a couple of notions, and some of them (zeros of a polynomial,
factorization, elimination) are hardly possible to fully understand in the case of
younger learners – for the first glance at least.
Despite that, I am fully convinced that all of the topics above can be discussed with almost anyone
at the appropriate level. Of course, we should not mention irreducible factorization
for the youngest learners (who are not familiar with the concept of breaking down of molecules into atoms yet),
but should do that for the prospective teachers. In some sense, the next generation
of teachers may and should have their ways to translate the beauty and usefulness
of mathematics for the next generation.
In worst case, a prospective teacher must completely skip the mathematical background
when using the LEGO kit or other means when introducing the concept of drawing linkages.
I agree that it can be very challenging to explain any ideas on the
correspondence between factorization, and that multiple essentially different curves can be
drawn with the same linkage body – as it is for Hart's A-frame.
Nevertheless, the drawing process is reproducible for everyone.
Even for the youngest learners at the primary level. If we can communicate just a little bit more
than "we are drawing something unusual but useful and beautiful",
we already gave our young learners an insight what STEAM is about.
Acknowledgements
The author was partially supported by a grant
PID2020-113192GB-I00 from the Spanish MICINN.