Software presentation at ISSAC'21
Automated reasoning tools in GeoGebra Discovery
by Zoltán Kovács, Tomás Recio and M. Pilar Vélez



ongoing work with Róbert Vajda and Christopher W. Brown
Abstract
We present some current achievements in the software package GeoGebra
Discovery that provides
several symbolic tools and commands to mechanically discover (and verify symbolically) relationships
on planar geometry constructions.
Our presentation includes the novel Discover and Relation
and Relation 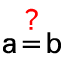 tools, and the Compare command.
tools, and the Compare command.
Our proposal successfully makes the cycle ‘conjecturing-checking-proving’ in elementary geometry even more accessible for general users, focusing not only on educational uses but research as well.
Our presentation includes the novel Discover
Our proposal successfully makes the cycle ‘conjecturing-checking-proving’ in elementary geometry even more accessible for general users, focusing not only on educational uses but research as well.
After 5 years...

We have worked towards having the program GeoGebra itself formulating
automatically the properties holding on a given
figure, without requiring practically no user intervention. This is achieved through two user tools:
- Discover
 and
and
- Relation
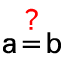 ,
,
- Compare (to obtain a general ratio between two expressions).
We are dealing with mathematically rigorously true statements (not just probabilistic or approximately correct).
Algorithmic summary
Roughly speaking, given a planar geometry construction with
- free points \(F_1, F_2, \ldots\),
- points \(D_1, D_2\),
- segments \(s_1, s_2, \ldots\),
- lines \(l_1, l_2, \ldots\) and
- circles \(c_1, c_2, \ldots\),
See
- Chou: Mechanical Geometry Theorem Proving. Springer, 1987.
- Kovács-Recio-Vélez: Detecting truth, just on parts. Revista Mat. Compl., 32, 2019.
Example 1: Discovery in a regular nonagon
Instead of issuing the command Discover(J) in this web interface,
the preferred method is to download
the desktop application and open the figure as a .ggb file (or redraw it, see below).
Timings: 50 seconds (web interface) or 5 seconds (desktop application) on an Intel(R) Core(TM) i7-8550U CPU @ 1.80GHz.
Construction protocol (if you want to redraw the figure from scratch)
| No. | Name | Toolbar Icon | Description | Value |
|---|---|---|---|---|
| 1 | Point A | A = (1, 1) | ||
| 2 | Point B | B = (2, 1) | ||
| 3 | Polygon poly1 | Polygon(A, B, 9) | poly1 = 6.18 | |
| 4 | Segment q | Segment B, D | q = 1.88 | |
| 5 | Segment r | Segment C, G | r = 2.88 | |
| 6 | Point J | Intersection of q and r | J = (2.5, 1.87) | |
| 7 | Segment p | Segment A, J | p = 1.73 |
Example 2: Obtaining a relation in a regular nonagon
Go back to Example 1, press Undo, Redo, unhide \(p\), select the
Relation 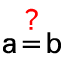 tool, then compare \(p\) and \(f\).
tool, then compare \(p\) and \(f\).
Example 3: Using the JavaScript Application Programming Interface (API)
Press F12 in the web browser to launch Developer Tools, select the Console tab, then type
- ggbApplet.evalCommand("result=Compare(p,f)")
- ggbApplet.getValueString("result")
Behind the scenes
Discovery algorithm
- Analyze all points to determine whether they are the same as another point.
- Examine all possible point triplets for collinearity.
- Check all possible 4-point subsets on the figure for concyclicity.
- With knowledge of the collinear points, define separate lines and determine whether they are parallel.
- Consider all possible point pairs and identify congruent segments.
- Determine perpendicular lines.
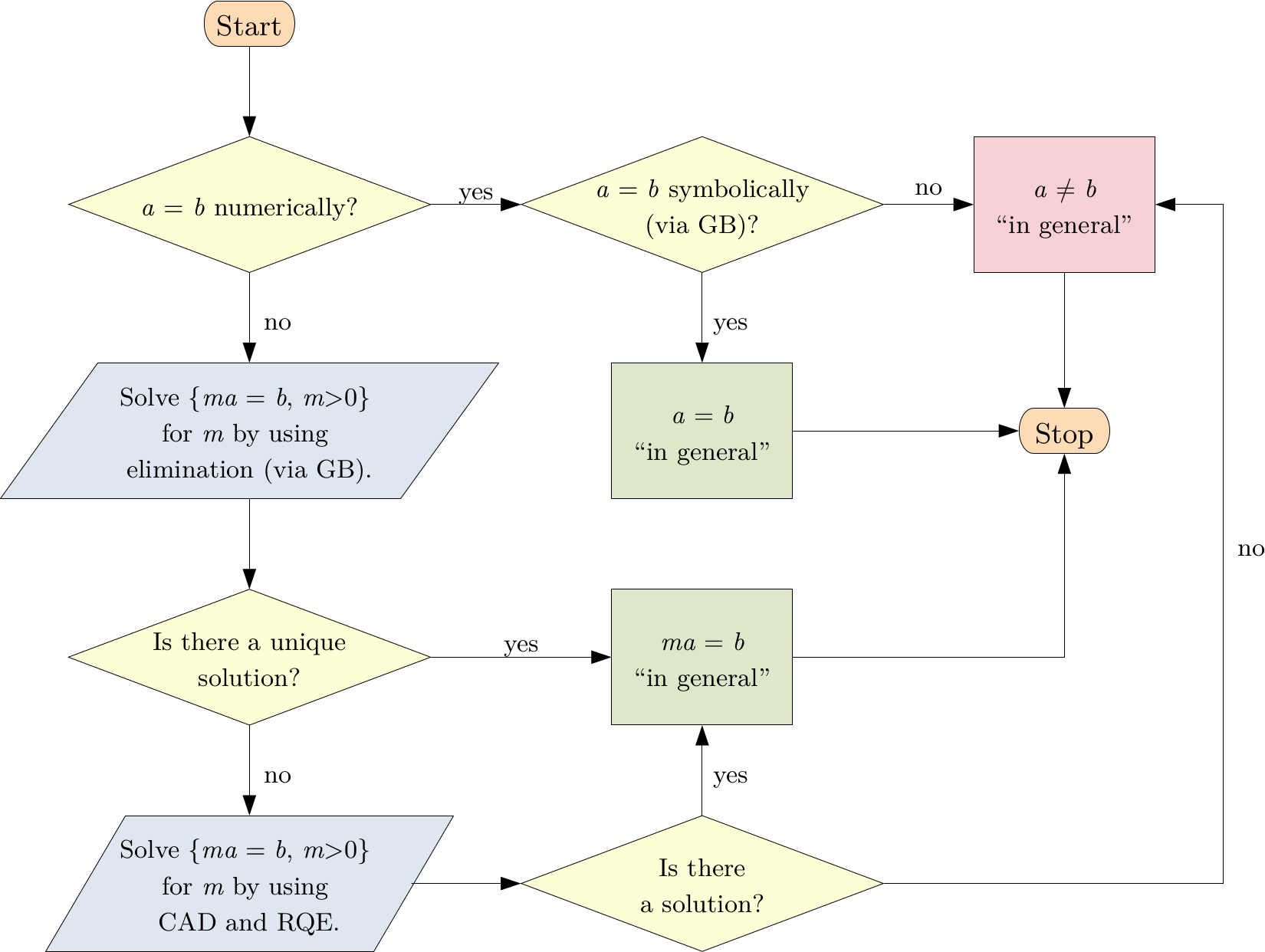
Relation algorithm (to compare \(a\) and \(b\))
Acknowledgements
The authors were partially supported by a grant MTM2017-88796-P from the Spanish MINECO (Ministerio
de Economia y Competitividad) and the ERDF (European Regional Development Fund).