2023. december 10.
JGEX 0.81
Ebben a blogbejegyzésben a Java Geometry Expert (JGEX) 0.81-es verziójáról lesz szó,
melynek kiadása 2023. december 10-ére, Szilassi Lajos matematikus kollégám 81. születésnapjára esik.
A 0.81-es verzió főként a magyar nyelvre való átültetést célozza meg. A fordítási
munkát az FSF.hu Alapítvány támogatta
a 2023-as
Szabad Szoftver Pályázat keretében.
A program a GitHubról
ingyenesen letölthető mind Windows, Mac és Linux rendszerekre.
A JGEX elemi geometriai bizonyításokban segít. Három kínai matematikus fejlesztette ki a
2000-es évek elején a világhírű
kínai elemi geometriai iskolai képzésre alapozva és azt tovább támogatva. (Elég ha csak
a Nemzetközi Matematikaolimpiákra gondolunk, ahol Kína az elmúlt 25 évben mindig
dobogós helyen végzett, az elmúlt
5 évben pedig első helyen: ezeken a versenyeken mindig van geometriai feladat is.)
A JGEX több bizonyítási módszert is támogat: ezek közül az egyik a Wu-módszer, ami a 80-es években
keltette fel az érdeklődést, mert a szoftver első számú szerzője,
Chou professzor 512
geometriai tétel automatikus bizonyítására alkalmazta azt. Chou könyve,
az 1988-ban kiadott Mechanical Geometry Theorem Proving
jelentős visszhangra talált, és több új módszer valamint újszerű kutatási irányok
megalapozását tette lehetővé.
A JGEX egyrészt tehát egy geometriai rajzolóprogram (a ma talán leginkább elterjedt
GeoGebrához is hasonlít), amelybe a Wu-módszer,
valamint egy ahhoz hasonló, az ún. Gröbner-bázisokon
alapuló algebrai technika,
továbbá egy adatbázis alapú (GDD elnevezésű) és egy ún. teljes szög módszer lett beépítve.
Tanárok számára egy további funkció, hogy kézzel is létrehozhatunk magyarázó prezentációkat
iskolai órák, szakkörök illusztrálására.
A másik két szerző Gao professzor (a Kínai Akadémia elismert tudósa) és
Ye professzor.
Gao Chou-val és egy korábbi társszerzővel, Zhang-gal a 90-es évek derekán a JGEX elődjén,
a Geometry Experten (rövid nevén a GEX-en) dolgozva vált ismertté, de munkájukat főként az amerikai
Wichita State University támogatása kísérte. A JGEX fejlesztése 2004 és 2010 közé tehető,
ezután a szerzőhármas két cikkben számolt be a kutatás eredményéről, majd hosszabb szünet után
a szoftver forráskódját 2017-ben tették közzé. A kódon azóta kevés változtatás történt,
ami részben az időközben hanyatlani látszó Java technológiának is köszönhető (gondolva itt arra is,
hogy a weboldalakba beágyazható Java appletek az elmúlt években teljesen eltűntek, hiszen
a böngészők ezt már nem támogatják). A JGEX által biztosított módszerek azonban továbbra
is úttörő jellegűek, és más szoftverek vagy egyáltalán nem, vagy csak részben voltak képesek
arra, hogy ezeket az új módszereket támogassák.
Nézzünk egy konkrét geometriai feladatot, amelyet a JGEX-szel tanulmányozhatunk! A programot
elindítva állítsuk át a nyelvet magyarra (ezt az Options > Preferences > Mode > Language menüpontok
alatt találjuk, majd a Hungarian opciót választva a Save Preferences-re kattintás
után a program kilép, s újra kell indítanunk). Ekkor, már a magyar felületen
töltsük be a Példák > JAR > simson demófájlt (vigyázzunk: két ilyen nevű is van,
az elsőt kell kiválasztani).
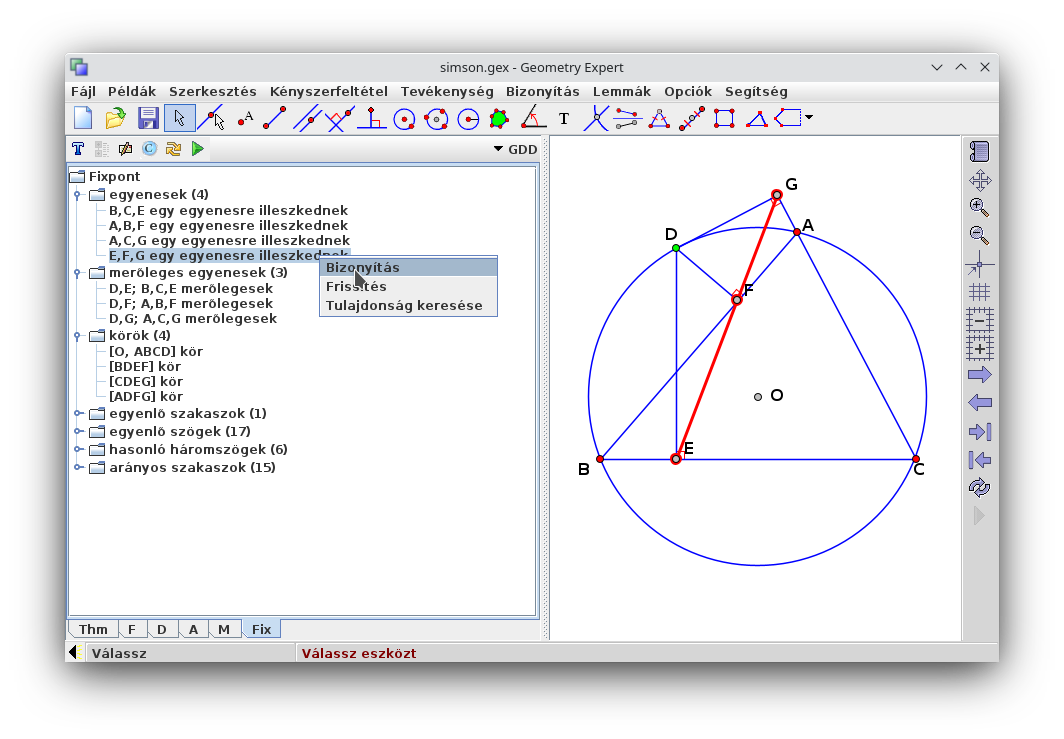




A képernyő jobb oldalán látható a szerkesztő terület, amelyben a menüsor alatti szerkesztő
eszközökkel, valamint a Szerkesztés menüben található további menüpontokkal hozhatunk létre
geometriai alakzatokat. Ha ezzel megvagyunk (példánkban nem kell tennünk semmit, minden készen áll),
a képernyő alján látható Fix lapra kattintva jeleníthetjük meg azokat a (numerikus módon
összegyűjtött) tulajdonságokat, amelyeket később szigorú matematikai eszközökkel is beláthatunk. Válasszuk
a Fixpont > egyenesek listából az utolsót, ami azt állítja, hogy az E, F és G pontok
egy egyenesre illeszkednek. Ez általánosságban valóban így van: ez az ún. Wallace-Simson tétel,
ami kimondja, hogy bármely háromszög körülírható köréről vett pontot az oldalegyenesekre levetítve
olyan talppontokat kapunk, amelyek egy egyenesre esnek. A JGEX ezt úgy fogja nekünk belátni, ha
a jobb egérgombbal az állításra kattintunk, majd a Bizonyítás opciót választjuk.

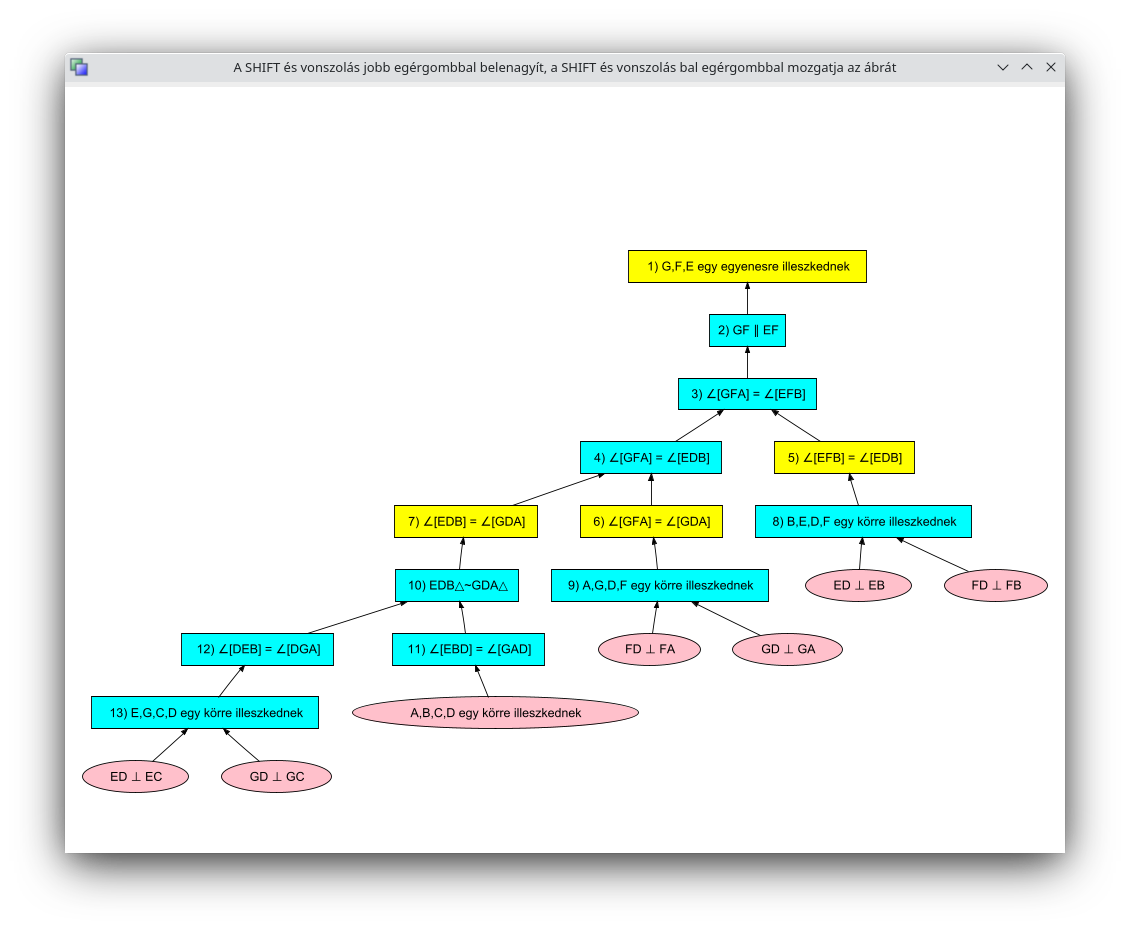
Alapértelmezésben a GDD-módszer indul el. Ez diákok számára a leghasznosabb, mert olyan formában
mutatja a bizonyítás lépéseit, ahogyan az iskolában is tanuljuk. Tanítványaimmal (akiket a
Linzi Katolikus Tanárképző Magánfőiskolán tanítok), köztük szakdolgozómmal, Alexander Vujic-csal arra
jutottunk, hogy a program által eredetileg lineárisan bemutatott bizonyítást grafikusan is illusztrálni
lehetne. A fent bemutatott bizonyításfa már ennek a tervnek egy előzetes prezentációja. Lent
egy egyszerűsített verzió is látható, ami ugyancsak velük készített közös munka, a kínai kollégák
korábbi fejlesztésének továbbgondolása:

Mint lentebb látható, a GDD-módszerhez hasonló kimenetet ad a teljes szög módszer, de ez utóbbi egy lineáris bizonyítás, ahol
egy bizonyos szögről akarjuk megmutatni, hogy az 180 fok, és algebrai lépéseken keresztül
vezetjük azt le (a ∠[0] jelenti a módszer jelölésrendszerében a 180 fokot):

(Ezt a kimenetet úgy lehet előhozni, hogy a GDD-re állított bizonyítástípust (fent, középen)
Teljes-re kell átállítani, majd a ▶ gombot megnyomni.)
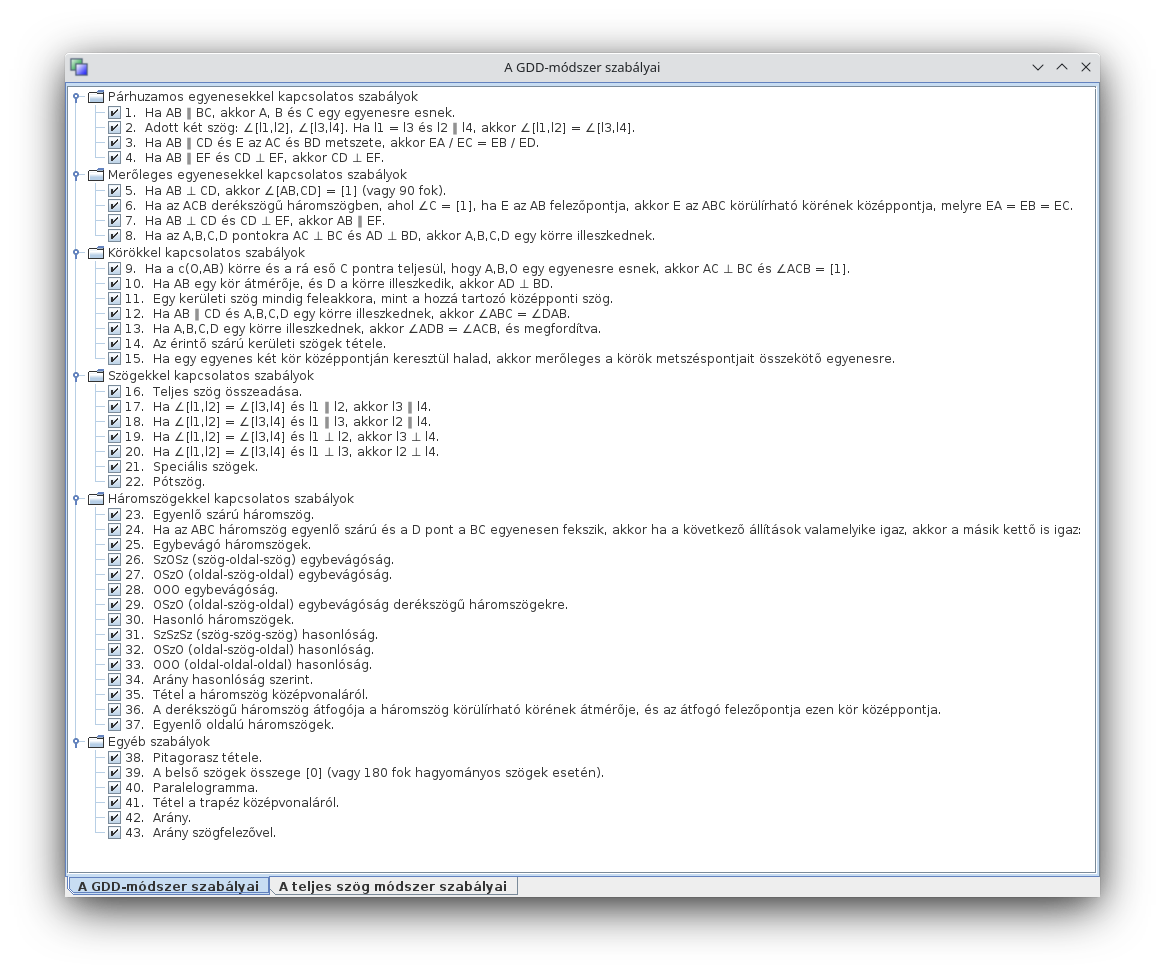
Mind a GDD-módszer, mind a teljes szögön alapuló bizonyítás egy-egy szabályrendszeren alapul.
A GDD-módszer esetében 43, a teljes szög módszernél 29 szabály van, amelyeket a program kombinatorikus
módon addig építget össze, míg egyszercsak a helyes gondolatmenet teljes egésze felépül. A JGEX
(és az automatikus bizonyító rendszerek általában) tehát nem egy előre betanult bizonyítást bifláznak
vissza, hanem minden egyes inputhoz intelligens módon (akárcsak a mesterséges intelligencia)
összegyűjtik azokat az érveket, amelyek a bizonyításban szerepet játszanak, és abból
szigorú logikai lépéseken keresztül egy teljes értékű, hézagmentes érvelést építenek fel.
A következő ábrán a GDD-módszer 43 szabálya látható, melyeket a Lemmák menüben tekinthetünk át:

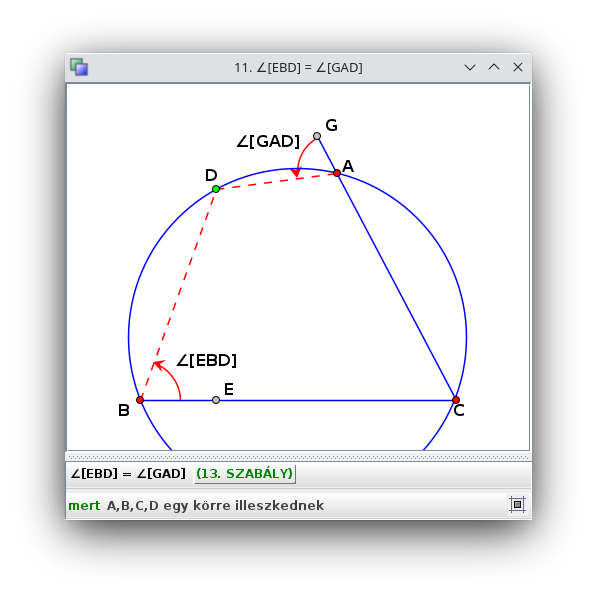
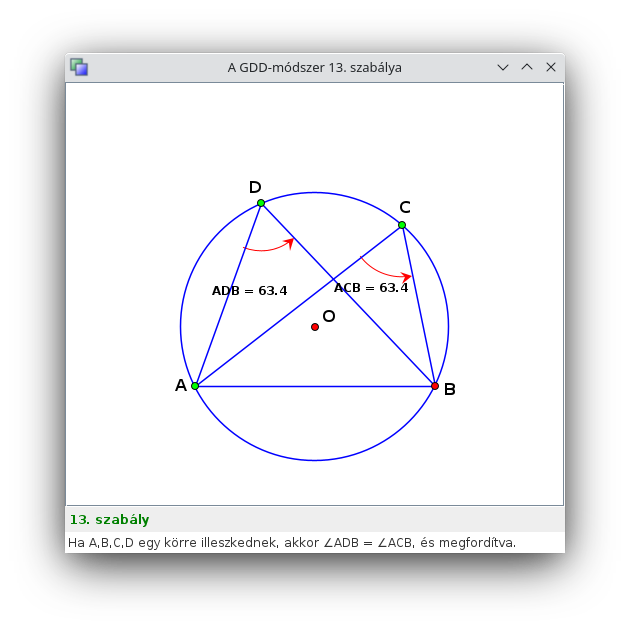
Ezek közül néhányat a fenti bizonyítás is említ. Pl. a 11. lépésben a 13. szabályt hozza
az automatikusan legyártott érvelés:

A 13. szabály nem más, mint a kerületi szögek tétele:

További bizonyítási módszerek
Két további bizonyítást mutatunk be. Mindkét típus ún. algebrai reprezentációval
dolgozik, ami annyit jelent, hogy a geometriai feladatot először koordinátageometriai feladatként
elemezzük, amelynek során az egyes pontok koordinátáit egy-egy változóval címkézzük fel.
Az első két pont koordinátáit fixáljuk (rendszerint \((0,0)\)-ra és \((0,1)\)-re, vagy ha nagyon óvatosak
akarunk lenni, a második pont y-koordinátáját \(x_4\)-gyel jelöljük), a többi pontét
pedig igyekszünk a szerkesztés lépéseit teljes körűen figyelembe véve olyan egyenletekkel leírni,
ahol csak polinomegyenlőségek szerepelnek. Ez valamelyest megköti a kezünket (mert nem lehet
pl. szakaszokról beszélni, csak egyenesekről), de a módszer meglepően sokrétű és rendkívül hatékony.
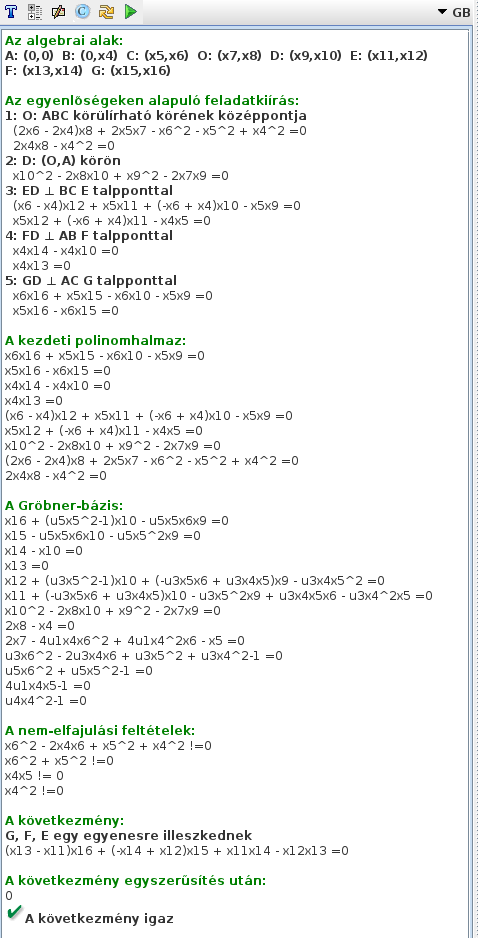
Az egyik ilyen algebrai reprezentációs módszer Gröbner-bázisokon alapul, amely a kapott
polinomegyenleteket hatékonyan tudja olyan formára hozni, ahol a következmény (itt az egy egyenesre
illeszkedés) már könnyen leolvasható. A Gröbner-bázis módszer nagy számításigényű lehet, ha
sok a változó, ezért bonyolultabb feladatokon még akkor is elvérezhet, ha amúgy az implementáció
hatékony. A JGEX-ben egy közepesen hatékony implementáció áll rendelkezésre, ami a Wallis-Simson
tétel esetében kiválóan működik, ahogyan ez a képen is látható (a bizonyítástípust itt GB-re
állítottuk, majd a ▶ gombot újra megnyomtuk):

Egy másik, a fentinél gyorsabb módszer a Wu-eljáráson alapuló technika. Ez sok esetben gyorsabb,
mint a fenti, de bizonyos információkat (amelyek elárulhatják, hogy az állítás mely szélsőséges
esetekben nem teljesül) nem feltétlenül tud feltárni. Az alábbi kép jól mutatja, hogy a számítás
valamelyest leegyszerűsödik:

Látszik azonban, hogy itt nem tártuk fel, hogy mik az elfajuló esetek.
A jövőbeli fejlesztésekről
A 2023-as ADG konferencia Belgrádban
került megrendezésre, ahol a JGEX továbbfejlesztéséről,
oktatási használatának lehetőségeiről több előadásban is szót ejtettünk. Reméljük,
hogy a ma megjelent új verzió egy fontos mérföldkő lesz abban, hogy az elemi geometria szépségét és
kihívásait modern módon tálaljuk az új generációk számára. Köszönettel tartozunk mindenkinek,
aki munkájával mindehhez hozzájárult.
Természetesen örömmel várjuk a visszajelzéseket is! A JGEX
Google Csoportban nagy érdeklődéssel fogadjuk a konstruktív és kritikus hozzászólásokat,
melyeket igyekszünk figyelembe venni a program új verzióinak tervezésekor.
A 0.81-es verzióról
Zárásképpen néhány technikai jellegű információ, csak szakmabelieknek. A fő kihívás az
Apache Ant-on
alapuló build rendszer Gradle-re
történő átírása, a táblázatszerűen megadott mintegy 500 kifejezés
gettext alapra konvertálása és további
300 frázis felvétele volt. Jelen pillanatban a magyar nyelv a leginkább támogatott
(az angol eredetivel egyetemben), mert az új fordítások a párhuzamosan rendelkezésre álló
fárszi, kínai, német, olasz, portugál és szerb nyelvekhez még nem készültek el.
Az új verzió elkészültéhez a programot számos helyen kisebb-nagyobb bővítésekkel kellett ellátni,
néhány helyen módosítani. A munka eredményeképpen Windows, Mac és Linux rendszereken könnyen indítható
telepítők is rendelkezésre állnak. A kb. 100 commitból álló módosítássorozatra 2023 novemberében
és decemberében került sor a szerző és Kovács Benedek munkájának eredményeképpen.

|
Zoltán Kovács Linz School of Education Johannes Kepler University Altenberger Strasse 69 A-4040 Linz |